What am I seeing?
Axis (gold) is the unit vector k. v (red) is split into:
- v∥ (teal): the component along the axis
- v⊥ (blue): the component perpendicular to the axis
Rodrigues says rotation keeps v∥ fixed and rotates v⊥ in the plane perpendicular to k.
Why this matters
This is the workhorse of 3D rotations: robotics, graphics, rigid body mechanics, Lie groups (SO(3)), and quaternion bridges.
It’s the “exponential map” in friendly clothing: R = exp(θK) for the skew matrix K.
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
How this connects
This matrix is generated from the same axis–angle data as Rodrigues’ formula. The exponential map
converts the skew-symmetric generator K into a proper rotation. Every frame preserves orthogonality and determinant 1 — the defining properties of SO(3).
1.000
0.000
0.000
0.000
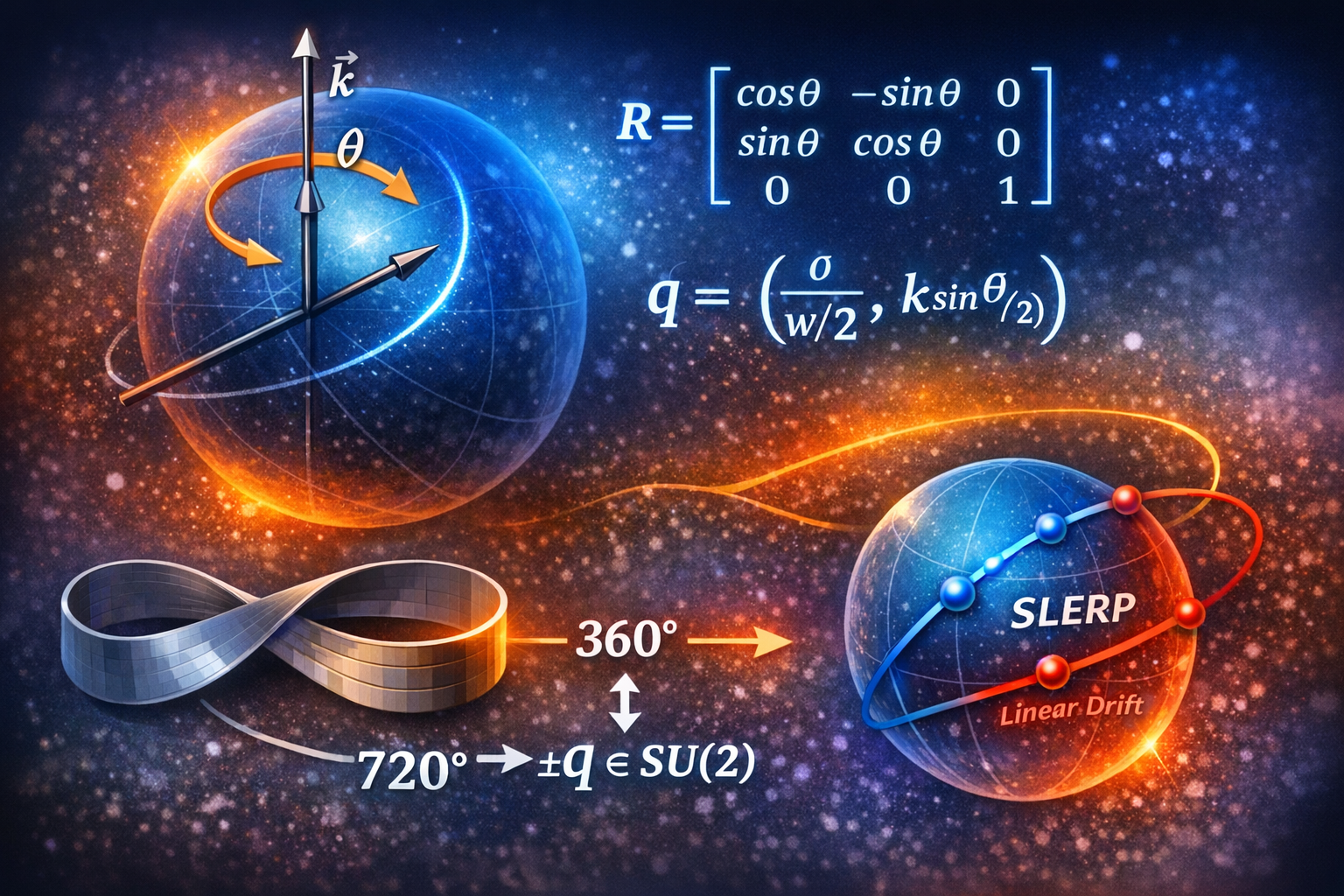
Why quaternions?
Quaternions encode rotations using a half-angle:
This avoids gimbal lock, interpolates smoothly, and reveals the double-cover of SO(3) by SU(2).
Opposite spinors q, −q ∈ SU(2)
What’s happening?
The mapping
identifies q and −q as the same physical rotation.
This is why spin-½ particles require a 720° rotation to return to their original quantum state.
Why this matters
Linear interpolation ignores the curvature of the rotation group. SLERP follows the geodesic on S³, preserving unit norm and rotational meaning.
This is why animation engines, spacecraft guidance, and quantum spin all use quaternions.
What you are seeing
A rigid object in SO(3) returns to its original orientation after 360°, but the path is twisted.
Only after 720° does the twist unwind continuously. This is why rotations lift naturally to SU(2), the double cover of SO(3).